Thinking is critical to learning! When our learning involves thinking, we not only understand what we are learning, but also have a much better chance of remembering it.
Before I explain the role of thinking in learning, I want to make sure that we are both on the same page when it comes to understanding what thinking is.
To do that, let me start by asking you a question!
What is common between a car and an aeroplane?
Immediately, you picture a car and an aeroplane and compare the two to find commonalities:
They are both modes of transportation, they both have wheels, they have engines, they have seats etc. etc.
Before I had asked you this question, were you thinking about a car and an aeroplane?
Definitely not! You weren’t thinking about cars and aeroplanes, but the moment I asked you the question, you (automatically) imagined a car and an aeroplane, and compared them.
Where did these mental images come from?
They came from a vast store of all the things we know (facts, ideas, what things look like, how to do something etc.) called Long Term Memory (LTM).
A long time ago (probably when you were a child), someone (your parents?) told you what a car is and what an aeroplane is. They pointed out a physical object and said this is a car. (they probably did that a few times on different occasions and then would have asked you to name the thing. This repeated association followed by questioning made this knowledge stick in your brain!)
So what has this got to do with understanding what thinking is?
Well, what you just did in response to my question is thinking! You pulled information about cars and aeroplanes that was stored in your LTM, put them side by side in your mind’s eye and compared them.
Let me give you another example of thinking!
Work out 12×3 in your mind.
Assuming that you learnt (and remember) how to do multiplication and know your times tables, you would follow the below steps (in your mind):
- multiply 2 and 3 and retrieve that fact that 2×3 equals 6 from your LTM (long term memory)
- remember that 6 is part of the solution
- multiply 3 and 1, retrieving the fact that 3×1 equals 3
- append the 6 to 3 to give you the answer 36
What you did to find the answer to 12×3 was thinking!
You received some information from the environment (I asked you to multiply 12 and 3)
In response to this information, you pulled the multiplication procedure and maths facts i.e. 2×3=6 and 3×1=3 from LTM and carried out the step to produce the answer 36.
Based on the above examples, thinking can be defined as mentally combining, comparing or manipulating information.
Note, the information that is used while thinking can come from our LTM, from the environment or both.
In the first example, in response to my question, all the information you used to determine the commonalities between a car and an aeroplane came from your LTM.
In the second example you used some information from the environment (the numbers and what procedure to carry out) and some from your LTM (how to multiply, maths facts).
And all this information was assembled and manipulated in what is referred to as Working Memory (WM). Thinking happens in WM!
When you are re-living a certain moment in your life, or wondering (while driving home) which dress to wear at your friend’s birthday, or trying to figure out who the murderer could be while watching a murder mystery, or calculating 12×3, or repeating a number to yourself while you look for a pen to write it down, you are using WM.
Here a diagram (by cognitive scientist Daniel T. Willingham) that shows the process of thinking:
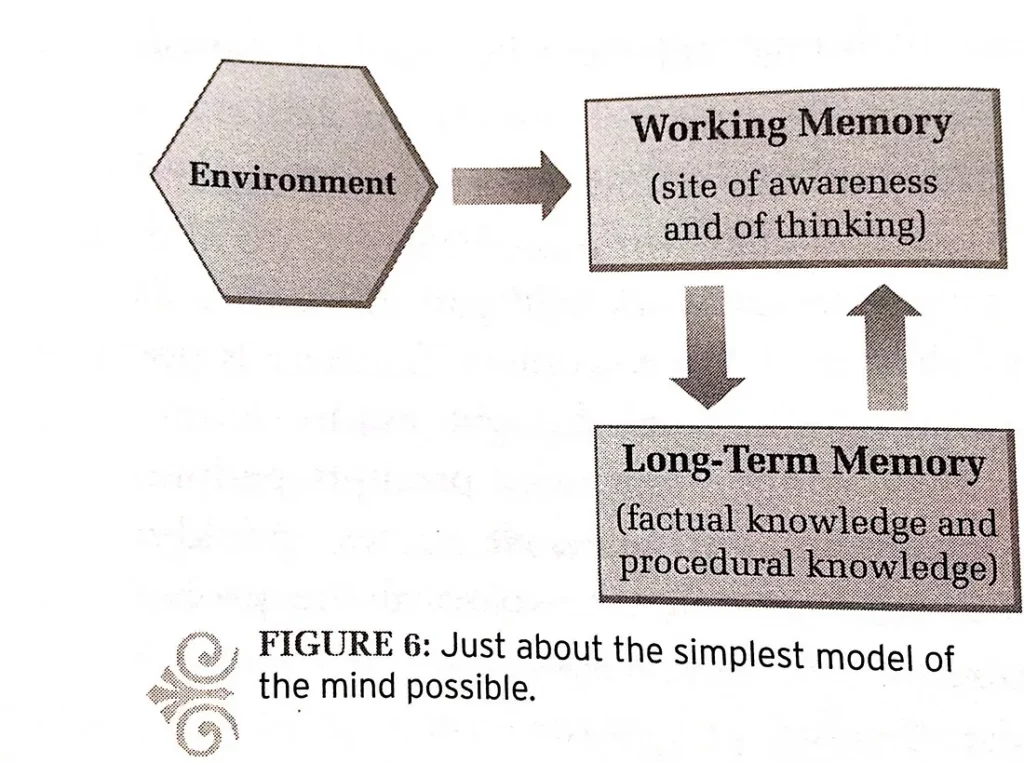
So hopefully, we are on the same page when it comes to our understanding of what thinking is!
Why is thinking necessary for learning?
What does it mean to learn?
Learning usually involves attaining a new bit of knowledge, developing a new understanding or the ability to do something.
Let’s take a simple example of vocabulary.
Here is a word ..
Cantankerous
I am pretty certain that most people reading this won’t know what cantankerous means!
Hmm … thoughts so far! (and if you did, hats off to you!)!
Cantankerous means streitsüchtig.
What! What does streitsüchtig mean? It means cantankerous, of course!
I am sure you are confused (as you should be) and thinking dammit, if you want me to understand what cantankerous means, tell me its meaning using words I am already familiar with!
Ohh sorry! Let me try again ..
Cantankerous means bad-tempered, argumentative, and uncooperative.
You get it, right?
Of course you do! You know what bad-tempered, argumentative and uncooperative mean. These words along with their meanings are already in your long-term memory.
So congratulations, you have just learnt something i.e., a new word. A word of warning though! This is only the first step in learning and if you stopped here, you most likely will forget the word and what it means soon! More about that later.
Let’s do a quick summary of what we have covered so far!
We said …
- Thinking is combining, comparing or manipulating information in working memory e.g. carrying out a calculation, figuring out a riddle, reading a sentence and trying to make sense of it
- Learning is the acquisition of new knowledge, developing a new understanding or the ability to do something e.g. learning a new word and its meaning, learning how to calculate the area of a triangle etc.
Now we are ready to consider the role that thinking plays in learning.
I introduced you to a new word ‘cantankerous’ and said it means bad-tempered, argumentative, and uncooperative. As you read these words their meanings, which were stored in your long term memory automatically and very quickly moved into your working memory, where you held the word ‘cantankerous’ and the words bad-tempered, argumentative, and uncooperative & their meanings together and created an association between them. This association in WM leads to the storing of the word ‘cantankerous’ in LTM and a link between this new memory and existing memories of bad-tempered, argumentative and uncooperative and their meanings.
I think another example would help!
Let’s say I introduce you to the concept of nominal scales by saying, a nominal scale is a measurement scale, in which numbers serve as “tags” or “labels” only, to identify or classify an object. In themselves, the numbers have no value.
Does that make sense? If you have never encountered this idea before then it probably does not make much sense.
So how do I make you understand this definition of a nominal scale? In other words, how do I get you to understand this concept?
I say, for example, numbers on the shirts of football or cricket players just act as labels to identify the players but other than that the numbers provide no other information. These numbers have no value.
Now the definition makes some sense, right?
I gave you some information i.e. the definition of nominal scales and then got you to connect that definition with something you already know i.e. shirts worn by players in a team which only act as labels or tags to identify those players but in themselves have no value (e.g. the number does not tell you anything about how good the player is, how long they have been with the team, what position he / she plays at etc.)
You now know what a nominal scale is. This understanding is not very deep but it’s a start. To make it deep I would need to give you more examples of nominal scales and also tell you about other scales of measurement such as ordinal scale (provides ordering or ranking information but not the difference between each rank e.g. finishing positions of runners in a race).
How you arrived at this (shallow) understanding is through thinking. You received information from the environment (you read the definition above), you were prompted to fetch relevant information from your long term memory into working memory (the idea of numbered shirts worn by players) and you held the two ideas together in WM and this led to understanding!

If no thinking was involved i.e. I did not prompt you to think about numbered shirts worn by players then the sentence would not make much of an impression i.e. if I asked you to recall what we learnt today, you would find it very hard to recall anything. You might manage to say that it was something to do with numbers and scales. You could memorise the definition I gave you and repeat it to me verbatim (rote knowledge) but that would be a lot of hard work and apart from being of no practical use, such memorisation does not lead to long term retention.
So, thinking not only helps us understand and thus makes what we learn useful (i.e. you could use this understanding to identify a nominal scale), but also makes what you learn stick in our brains.
PS. I realise that I haven’t explained how thinking leads to better retention! I will when I rework this article




